Time Series Forecasting: Machine Learning Approach#
In this section we are going to introduce some concepts related with time series forecasting from a practical Machine learning based perspective, following the Skforecast approach. To go deeper into the details is totally advisable to take a look to the Skforecast website: https://skforecast.org/0.11.0/index.html
A time series is a succession of chronologically ordered data spaced at equal or unequal intervals. The forecasting process consists of predicting the future value of a time series, either by modeling the series solely based on its past behavior (autoregressive) or by using other external variables.
Univariate forecasting#
Definition of the predictors and response#
In order to apply machine learning models to forecasting problems, the time series has to be transformed into a matrix in which each value is related to the time window (lags) that precedes it.
In a time series context, a lag with respect to a time step t is defined as the values of the series at previous time steps. For example, lag 1 is the value at time step t−1 and lag m is the value at time step t−m.
This type of transformation also allows to include additional (exogenous) variables.
Here we have a graphical example of a predictor matrix X and a response, with 5 lags, suitable to be apply in a time series forecasting scenario.
from PIL import Image
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p1.png').resize((700, 300)).convert("RGB")
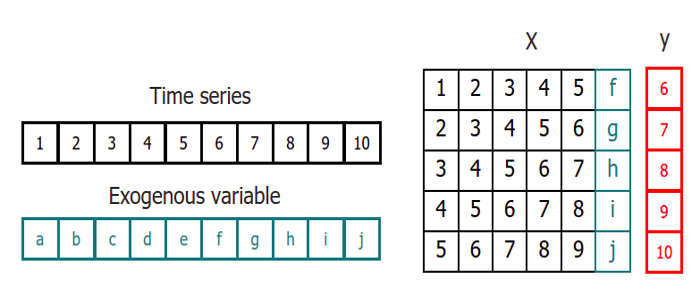
Once data have been rearranged into the new shape, any regression model can be trained to predict the next value (step) of the series. During model training, every row is considered a separate data instance, where values at lags 1, 2, … t are considered predictors for the target quantity of the time series at time step t+1 .
Forecasting processes#
When working with time series, it is seldom needed to predict only the next element in the series ( t+1 ). Instead, the most common goal is to predict a whole future interval (( t+1 ), …, ( t+n )) or a far point in time ( t+n ). Several strategies allow generating this type of prediction.
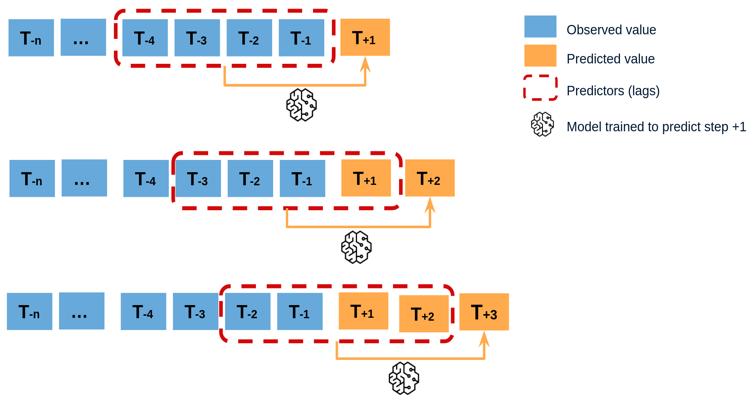
Recursive multi-step forecasting#
Since the value tn−1 is required to predict tn , and tn−1 is unknown, a recursive process is applied in which, each new prediction, is based on the previous one. This process is known as recursive forecasting or recursive multi-step forecasting.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p2.png').resize((750, 400)).convert("RGB")
Direct multi-step forecasting (several models)#
Direct multi-step forecasting consists of training a different model for each step of the forecast horizon. For example, to predict the next 5 values of a time series, 5 different models are trained, one for each step. As a result, the predictions are independent of each other.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p3.png').resize((750, 400)).convert("RGB")
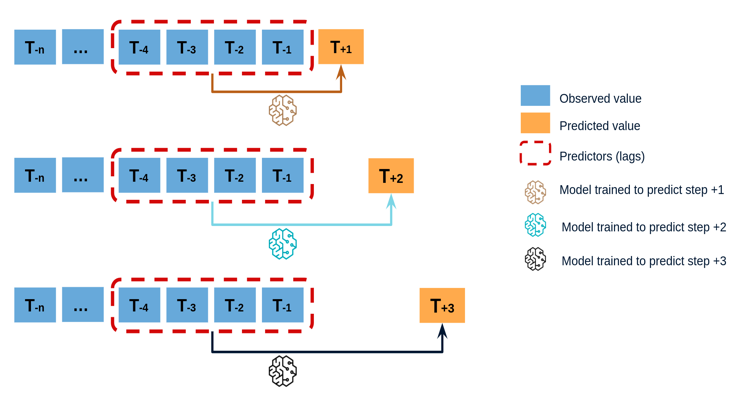
The main complexity of this approach is to generate the correct training matrices for each model. It is also important to bear in mind that this strategy has a higher computational cost since it requires the train of multiple models. The following diagram shows the process for a case in which the response variable and two exogenous variables are available.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p4.png').resize((900, 600)).convert("RGB")
Multivariate forecasting#
Multiple forecasting is also known as dependent multi-series forecasting
In dependent multi-series forecasting (multivariate time series), all series are modeled together in a single model, considering that each time series depends not only on its past values but also on the past values of the other series. The forecaster is expected not only to learn the information of each series separately but also to relate them. An example is the measurements made by all the sensors (flow, temperature, pressure…) installed on an industrial machine such as a compressor.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p7.png').resize((850, 500)).convert("RGB")

Since as many training matrices are created as there are series in the dataset, it must be decided on which level the forecasting will be performed.
In the below image we is represented a how multivariate forecasting works for predicting the Series 1 using a direct multi-step forecasting process.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p8.png').resize((750, 450)).convert("RGB")
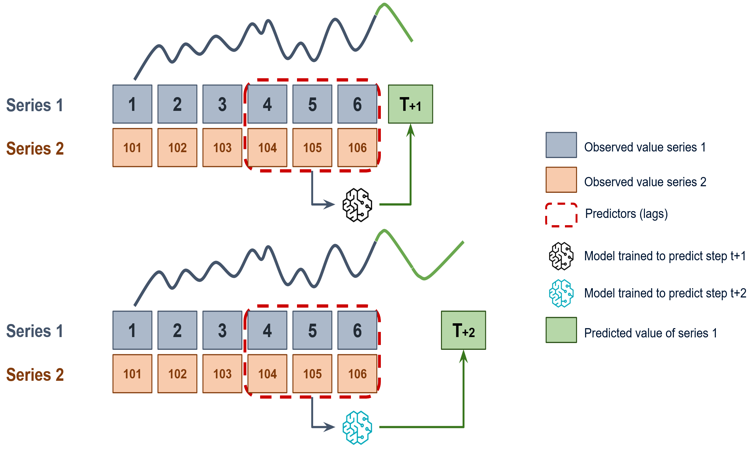
Multiple forecasting#
Multiple forecasting is also known as independent multi-series forecasting
In univariate time series forecasting, a single time series is modeled as a linear or nonlinear combination of its lags, where past values of the series are used to forecast its future. In multi-series forecasting, two or more time series are modeled together using a single model.
In independent multi-series forecasting a single model is trained for all time series, but each time series remains independent of the others, meaning that past values of one series are not used as predictors of other series. However, modeling them together is useful because the series may follow the same intrinsic pattern regarding their past and future values. For instance, the sales of products A and B in the same store may not be related, but they follow the same dynamics, that of the store.
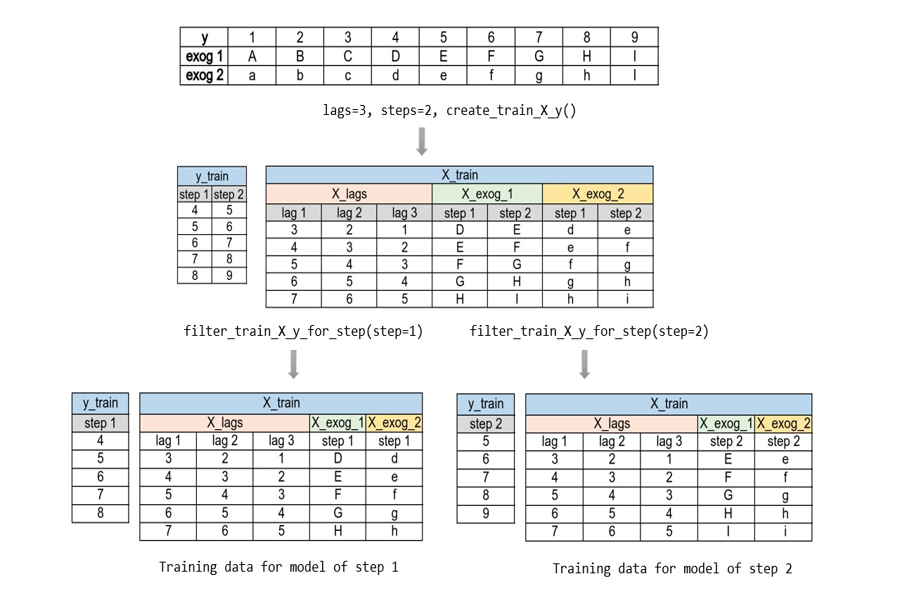
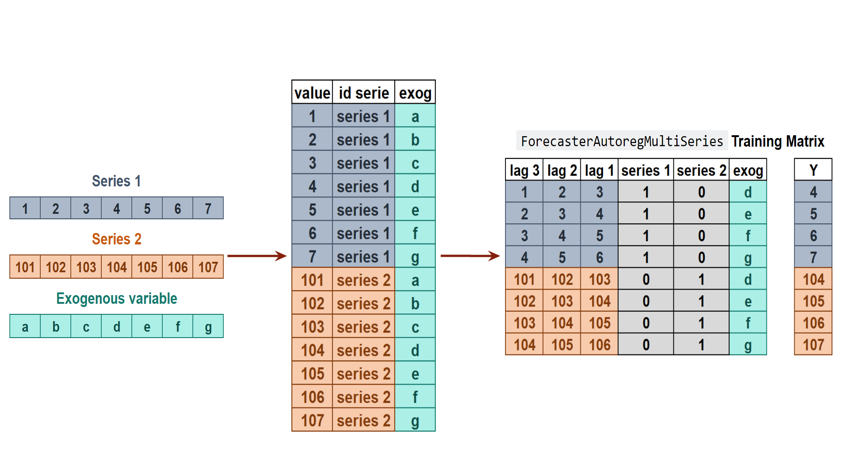
The following image explains the internal forecaster transformation of two time series and an exogenous variable into the matrices needed to train a machine learning model in a multi-series context.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p5.png').resize((850, 450)).convert("RGB")
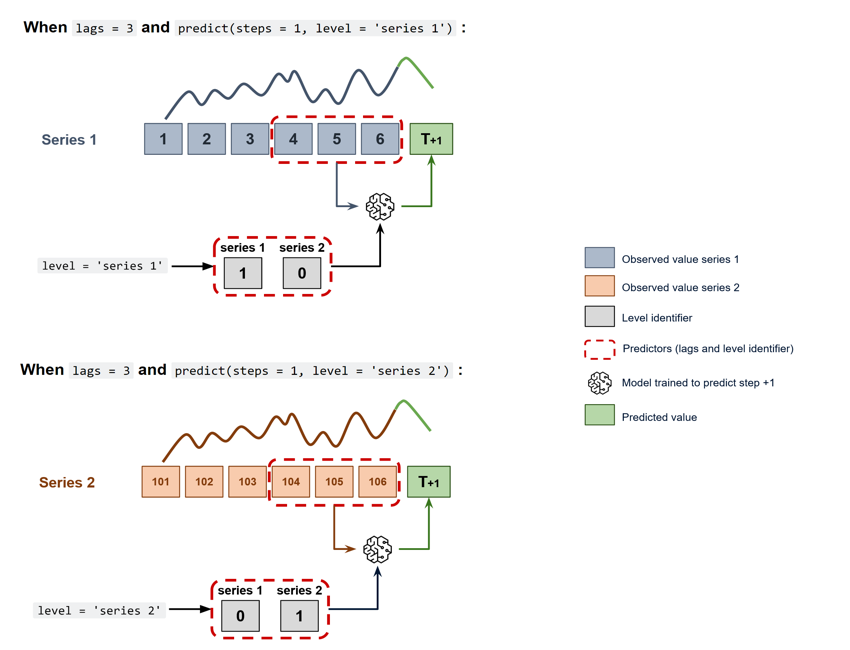
To predict the next n steps, the strategy of recursive multi-step forecasting is applied, with the only difference being that the series name for which to estimate the predictions needs to be indicated.
Image.open(r'C:\Users\fscielzo\Documents\DataScience-GitHub\Time Series\Temperature Prediction\Second Project\images\p6.png').resize((850, 650)).convert("RGB")
About the use of exogenous variables#
In certain scenarios, it is possible to have information about other variables, whose future value is known, so could serve as additional predictors in the model.
The future information about the exogenous variable must be available when making predictions.
